Some electrical temperature gages I bought (Autometer Sport- and Pro-Comp) turned out to be quite inaccurate when I tested them in a pot of hot water with a laboratory thermometer. I hooked the suspect gage up to a variable power supply (set at 13.5V) and brought the water temperature from room temperature through boiling (near sea level, with the thermometer showing 212 deg. F) and made note of the thermometer reading (independent variable), gage reading, and sender resistance (dependent variables).
I determined that the a few of these gages were reading in the area of 20 degrees too low. I tried varying the supply voltage, but the levels didn't change drastically, maybe a few degrees indicated on the gage. The Autometer gages have no calibration screws, etc. available to change the gage readings. They can be disassembled by de-crimping the bezel, but this is messy and prone to damaging the gage bezel.
I also have retained the stock fuel tank and sender in my 240Z, but wanted to use a matching Autometer Pro-Comp Fuel level gage. Well, Autometer doesn't have a fuel level gage that works with the range of resistance that the Datsun fuel sender has from Empty to Full (I measured mine to be 88 ohms Empty, and 8 ohms Full). However, the one for the older FORD fuel senders is close to this range (73 ohms Empty and 8-12 ohms Full).
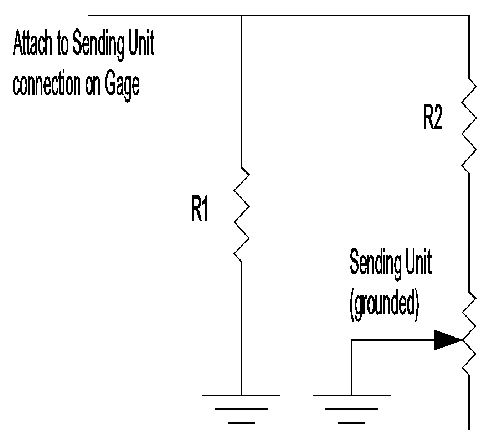
Both the temperature and fuel level gages work on a varying resistance input - the sending units are variable resistors. One side of the varying resistance is grounded in both cases, and the other side is connected through the wiring harness to the "S" terminal on the Autometer gage.
I devised a method to "calibrate" the gages with a couple of resistors connected to the external terminals as shown in the figure below. One resistor (R1) changes the sensitivity of the gage/sending unit set and the other (R2) corrects any offset error due to this sensitivity change.

Depending on the system being calibrated, the sending unit is either the temperature sending unit or the fuel level sender.
So R2 can be put in line (in series) any where between the sending unit and the "S" connection on the gage.
R1 is connected across the "S" connection on the gage and ground.
So how do you know what values of resistors to put in for R1 and R2?
Ohm's Law and A Little Algebra
...That's how. The circuit above is a way of taking the resistance at from the Sending Unit and changing it in a way such that the gage "S" terminal sees a different resistance. Ohm's law can be shown to give the following relationships between a pair of series resistors and a pair of parallel resistors to give an effective resistance for the pairs (Reff):
Two series resistors (R2 and the sending unit, RS, in our case) : Reff(s) = R2 + RS
Two parallel resistors, Ra and Rb: Reff(p) = (Ra * Rb)/(Ra + Rb)
So for the circuit above, use the formula for parallel resistors and let Ra = R1, and let Rb=Reff(s)=R2+RS:
Reff = (R1*(R2+RS))/(R1+R2+RS)
Now, to do anything useful with this result, you need some data. The data is the resistance needed to make the gage read correctly for a chosen temperature gage reading or indicated fuel level gage reading (to use for Reff in the last equation), and the actual resistance that the sending units exhibit at the chose temperature or fuel level sending unit postion. Actually, you need to choose two gage readings you want to have the gage read correctly at. We have two unknowns (R1 and R2) and therefore we need two equations - one for a "low" reading and one for a "high" reading. I'll refer to these two required resistances as R(gage-low) and R(gage-high) from here on. Note that this circuit will only ensure that the gage reads correctly at these two gage readings, but it should be pretty accurate in the range between these readings if the gage and sender are at all linear in there variation through the range.
Getting Some Data to Work With
For the Fuel Level gage, this is a pretty simple decision. You want to know when the tank is empty and when it's full, so those are the positions of interest. Using a good variable resistor or fixed value resistors, determine what the resistances are that are needed to make the fuel level gage read Empty and Full, with a representative running voltage applied to the gage (as if the engine were running and the alternator was charging - I chose 13.5V as an average reading). Now you have R(gage-low) and R(gage-high) for the fuel level gage. Unfortunately, it appears that the gage will not read accurately between Empty and Full, but what fuel level gage in any car does!?
For the temperature gage, the same method applies. You need to choose two temperature readings that bound the range where you want the gage/sending unit pair to be accurate. I choose 180 and 210 deg F, as this is the range of engine operation of interest and it's hard to get plain water to above 212F! I didn't want to involve myself with coolant in the kitchenware! Besides, the gage has tick marks at 180 and 210 so it's easy to see if it's calibrated correctly, when calibrating the sending unit.
For the temperature sending unit, as noted in the first paragraph, I created a Mr. Wizard looking setup in my kitchen.
I had a variable power supply (to power the gage, as it would be wired into the car), a pot of water on the stove with the element of the temperature sending unit submerged, and wires running from the sending unit (ground and the connection for the gage) to the gage. In this way I could slowly bring the water up to temperature and see where the gage read 180F, disconnect the sending unit, and measure it's resistance. This I used for R(gage-low). I'd then get the water to 180F and measure the resistance of the sending unit. This is R(sender-low). Repeat this procedure to find the resistance of the sender to make the gage read 210F, R(gage-high), and the resistance of the sending unit at 210F, R(sender-high).
Now, if you find out that R(gage-low) and R(sender-low) are the same or withing say 10 or 20 ohms of another, stop right there - the gage is probably pretty close. Make the same comparison for R(gage-high) and R(sender-high). If these are close as well, the gage/sending unit pair are fairly accurate.
But my experience was different and I needed to calibrate the gages. I'm not going to drag you through the algebra of solving for R1 and R2, but suffice it to say there are square roots involved and it can get messy depending on the input data.
I've developed a Gage Calibration Spreadsheet (MS Excel 2000) to take the four pieces of input data, R(gage-low), R(gage-high), R(sender-low) and R(sender-high), and output R1 and R2.
Depending on the input data, sometimes R2 is not needed. Other times, there is no solution to the mathematical problem and no one or two resistors in this arrangement will calibrate the gage. For both the Sport-Comp and Pro-Comp water temperature gages I bought, only one resistor was needed, R1. The same goes for two temperature gage I calibrated for Mike Kelly. My fuel level gage required both resistors.
Hopefully, I've taken care of tests in the spreadsheet so that the user will either get actual resistor values, a flag that one or both resistor is needed (if either R1 or R2 is 0.0, then no resistor is needed in that position in the circuit) or a message saying that there is no solution to the problem and the gage/sending unit can not be calibrated in this fashion.
There is an allowed error that can be specified as to whether the effective resistance matches that needed by the gage. The circuit is then checked using R1 and R2 found for the R(sender-low) and R(sender-high) inputs, and the effective outputs are given and compared to the desired R(gage-low) and R(gage-high), respectively.
Of course, there are no gaurantees with this approach, but it has proven useful to Mike and I.